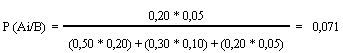teorema de bayes (tercer parcial)

 

El Teorema de Bayes viene a seguir el proceso inverso al que hemos visto en el Teorema de la probabilidad total:

Teorema de la probabilidad total: a partir de las probabilidades del suceso A (probabilidad de que llueva o de que haga buen tiempo) deducimos la probabilidad del suceso B (que ocurra un accidente).
Teorema de Bayes: a partir de que ha ocurrido el suceso B (ha ocurrido un accidente) deducimos las probabilidades del suceso A (¿estaba lloviendo o hacía buen tiempo?).

La fórmula del Teorema de Bayes es:

Tratar de explicar estar fórmula con palabras es un galimatías, así que vamos a intentar explicarla con un ejemplo. De todos modos, antes de entrar en el ejercicio, recordar que este teorema también exige que el suceso A forme un sistema completo.

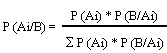
Ejercicio 1º: El parte meteorológico ha anunciado tres posibilidades para el fin de semana:

a) Que llueva: probabilidad del 50%.
b) Que nieve: probabilidad del 30%
c) Que haya niebla: probabilidad del 20%.

Según estos posibles estados meteorológicos, la posibilidad de que ocurra un accidente es la siguiente:

a) Si llueve: probabilidad de accidente del 10%.
b) Si nieva: probabilidad de accidente del 20%
c) Si hay niebla: probabilidad de accidente del 5%.

Resulta que efectivamente ocurre un accidente y como no estabamos en la ciudad no sabemos que tiempo hizo (nevó, llovío o hubo niebla). El teorema de Bayes nos permite calcular estas probabilidades:

Las probabilidades que manejamos antes de conocer que ha ocurrido un accidente se denominan "probabilidades a priori" (lluvia con el 60%, nieve con el 30% y niebla con el 10%).
Una vez que incorporamos la información de que ha ocurrido un accidente, las probabilidades del suceso A cambian: son probabilidades condicionadas P (A/B), que se denominan "probabilidades a posteriori".

Vamos a aplicar la fórmula:

a) Probabilidad de que estuviera lloviendo:

La probabilidad de que efectivamente estuviera lloviendo el día del accidente (probabilidad a posteriori) es del 71,4%.
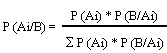
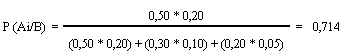
b) Probabilidad de que estuviera nevando:

La probabilidad de que estuviera nevando es del 21,4%.
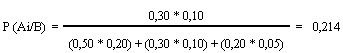
c) Probabilidad de que hubiera niebla:

La probabilidad de que hubiera niebla es del 7,1%.

tecnicas de conteo (tercer parcial )

Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Ejemplos en los que definitivamente haremos uso de las técnicas de conteo serían:
-¿Cuántas comisiones pro limpieza del instituto se pueden formar si hay 150 alumnos que desean ayudar en esta tarea y se desea formar comisiones de ocho alumnos?
-¿Cuántas representaciones de alumnos pueden ser formadas a) si se desea que estas consten solo de alumnos de Ingeniería Química?, b) se desea que el presidente sea un químico?, c) se desea que el presidente y tesorero sean químicos? Para todos los casos, se desea que las representaciones consten de once alumnos.
-¿Cuántas maneras tiene una persona de seleccionar una lavadora, una batidora y dos licuadoras, si encuentra en una tienda 8 modelos diferentes de lavadoras, 5 modelos diferentes de batidoras y 7 modelos diferentes de licuadoras?
Se les denomina técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las que a continuación se explicarán y hay que destacar que éstas nos proporcionan la información de  todas las maneras posibles en que ocurre un evento determinado.

DIAGRAMA DE ARBOL (TERCER PARCIAL)

Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades; consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final). Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

El diagrama de árbol va de lo general a lo especifico, es decir, parte de un problema general (el “tronco”) y continua con niveles subsecuentes o causas (las “ramas”).

Los diagramas en árbol son muy útiles para "fabricar" cualquier tipo de agrupación, ya sean variaciones, permutaciones o combinaciones.